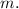Question

Find The slope between this two points:
(5,9),(-2,8)
​

Answer 1

`\boxed{\tt \: SLOPE= \cfrac{1}{7}}`

OR

`\boxed{ \tt\: SLOPE = 0.142}`

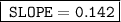
Explanation:

Given:

Two points, i.e.

`\tt \: (5,9),(-2,8)`

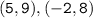
To Find:

The slope between the two given points.

Solution:

To Find out the slope between two points,we will use the formula of Slope, i.e. :

`\boxed{\rm \: m = \cfrac{y_ 2 - y_ 1}{x_2 - x_ 1}}`

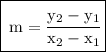
According to the Question,

`\rightarrow \: \rm \: y_2 = 8`

`\rightarrow \: \rm \: y_1 = 9`

`\rightarrow \: \rm \: x_2 = - 2`

`\rightarrow \: \rm \: x_1 = 5`

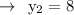
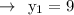
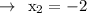
Now Substitute the values on the formulae of slope and then Simplify using PEMDAS rule :

`\rm \: \longrightarrow Slope = \cfrac{8 - 9}{ - 2 - 5}`

`\rm \: \longrightarrow Slope = \cfrac{ - 1}{ - 2 - 5}`

`\rm \: \longrightarrow Slope = \cfrac{ \cancel- 1}{ \cancel- 7}`

`\rm \: \longrightarrow Slope = \cfrac{1}{7}`

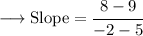
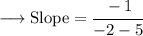
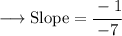
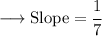
In Decimal,

`\rm \: \longrightarrow Slope =0.142`

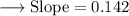
Hence, the slope between the two given points would be
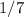`1/7` or
`0.142`.

`\rule{225pt}{2pt}`

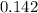I hope this helps!

Have a nice day! :)

Note:

SLOPE is usually denoted as
`m.`

Answer 2

The slope is 1/7.

Explanation:

Use the slope formula.

Slope:

`\Longrightarrow: \sf{(y_2-y_1)/(x_2-x_1)}`

• y2=8
• y1=9
• x2=(-2)
• x1=5

Rewrite the problem down.

`\sf{(8-9)/((-2)-5)=(-1)/(-7)=\boxed{\sf{(1)/(7)}}`

Dividing is another option.

1/7=0.142.

• Therefore, the slope is 1/7, which is our answer.

I hope this helps! Let me know if you have any questions.