Question

Service calls arriving at an electric company follow a Poisson distribution with an average arrival rate of 5656 per hour. Find the average and standard deviation of the number of service calls in a 1515-minute period. Round your answer to three decimal places, if necessary.

Answer 1

The average number of service calls in a 15-minute period is of 14, with a standard deviation of 3.74.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval. The variance is the same as the mean.

Average rate of 56 calls per hour:

This means that
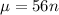`\mu = 56n`, in which n is the number of hours.

Find the average and standard deviation of the number of service calls in a 15-minute period.

15 minute is one fourth of a hour, which means that
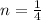`n = (1)/(4)`. So

`\mu = 56n = (56)/(4) = 14`

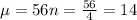
The variance is also 14, which means that the standard deviation is
`√(14) = 3.74`

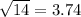
The average number of service calls in a 15-minute period is of 14, with a standard deviation of 3.74.