Answer:
5
Explanation:
The winnings are in G.P. : 1, 2, 4, ..... till 10 toss.
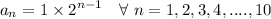
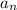 denotes the winnings on the
denotes the winnings on the
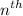 toss.
toss.
The probability of earning amount
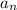 on the
on the
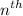 toss is =
toss is =
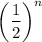
∴
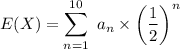

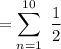
Sum of the 1st n terms of the A.P. is :
![$=(n)/(2)[2a+(n-1)d] $](https://img.qammunity.org/2022/formulas/mathematics/high-school/n7qk6sm2ij5d7xx9ycvp9d1y7750qu1u83.png)
![$=(10)/(2)[2* (1)/(2)+(10-1)* 0] $](https://img.qammunity.org/2022/formulas/mathematics/high-school/nekjsndoj4obno2iu5q0bi1vaope1wgj2b.png)
= 5
Therefore, E(X) = 5
Hence the expected value of the game is 5