Answer:
The diameter decreases at a rate of 0.053 cm/min.
Explanation:
Surface area of an snowball
The surface area of an snowball has the following equation:
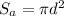
In which d is the diameter.
Implicit differentiation:
To solve this question, we differentiate the equation for the surface area implictly, in function of t. So
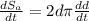
Surface area decreases at a rate of 3 cm2/min
This means that
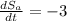
Tind the rate (in cm/min) at which the diameter decreases when the diameter is 9 cm.
This is
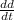 when
when
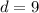 . So
. So
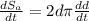

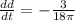
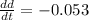
The diameter decreases at a rate of 0.053 cm/min.