Answer:
r₂ = 0.316 m
Step-by-step explanation:
The sound level is expressed in decibels, therefore let's find the intensity for the new location
β = 10 log
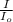
let's write this expression for our case
β₁ = 10 log \frac{I_1}{I_o}
β₂ = 10 log \frac{I_2}{I_o}
β₂ -β₁ = 10 (
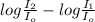 )
)
β₂ - β₁ = 10
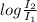
log \frac{I_2}{I_1} =
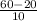 = 3
= 3
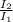 = 10³
= 10³
I₂ = 10³ I₁
having the relationship between the intensities, we can use the definition of intensity which is the power per unit area
I = P / A
P = I A
the area is of a sphere
A = 4π r²
the power of the sound does not change, so we can write it for the two points
P = I₁ A₁ = I₂ A₂
I₁ r₁² = I₂ r₂²
we substitute the ratio of intensities
I₁ r₁² = (10³ I₁ ) r₂²
r₁² = 10³ r₂²
r₂ = r₁ / √10³
we calculate
r₂ =
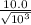
r₂ = 0.316 m