Answer
a) 62 percent
b) 40 percent
Step-by-step explanation:
Original diameter ( d
 ) = 10.33 mm
) = 10.33 mm
Original Gauge length ( L
 ) = 52.8 mm
) = 52.8 mm
diameter at point of fracture ( d
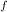 ) = 6.38 mm
) = 6.38 mm
New gauge length ( L
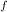 ) = 73.9 mm
) = 73.9 mm
Calculate ductility in terms of
a) percent reduction in area
percentage reduction = [ (A
 - A
- A
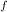 ) / A
) / A
 ] * 100
] * 100
A
 ( initial area ) = π /4 di^2
( initial area ) = π /4 di^2
= π /4 * ( 10.33 )^2 = 83.81 mm^2
A
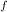 ( final area ) = π /4 df^2
( final area ) = π /4 df^2
= π /4 ( 6.38)^2 = 31.97 mm^2
hence : %reduction = ( 83.81 - 31.97 ) / 83.81
= 0.62 = 62 percent
b ) percent elongation
percentage elongation = ( L
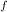 - L
- L
 ) / L
) / L

= ( 73.9 - 52.8 ) / 52.8 = 0.40 = 40 percent