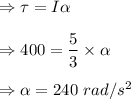Question

A horizontal 2.00\ m2.00 m long, 5.00\ kg5.00 kg uniform beam that lies along the east-west direction is acted on by two forces. At the east end of the beam, a 200\ N200 N forces pushes downward. At the west end of the beam, a 200\ N200 N force pushed upward. What is the angular acceleration of the beam

Answer 1

Answer:
`240\ rad/s^2`

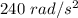
Step-by-step explanation:

Given

Length of beam
`l=2\ m`

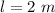
mass of beam
`m=5\ kg`

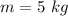
Two forces of equal intensity acted in the opposite direction, therefore, they create a torque of magnitude

`\tau =F* l=200* 2=400\ N.m`

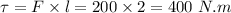
Also, the beam starts rotating about its center

So, the moment of inertia of the beam is

`I=(ml^2)/(12)=(5* 2^2)/(12)\\\\I=(5)/(3)\ kg.m^2`

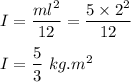
Torque is the product of moment of inertia and angular acceleration

`\Rightarrow \tau=I\alpha\\\\\Rightarrow 400=(5)/(3)* \alpha\\\\\Rightarrow \alpha =240\ rad/s^2`