Answer:
No, there is not sufficient evidence to support the claim that the bags are underfilled
Explanation:
A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 434 gram setting.
This means that the null hypothesis is:
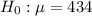
It is believed that the machine is underfilling the bags.
This means that the alternate hypothesis is:
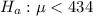
The test statistic is:
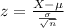
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
434 is tested at the null hypothesis:
This means that
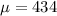
A 9 bag sample had a mean of 431 grams with a variance of 144.
This means that
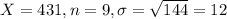
Value of the test-statistic:
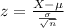
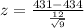
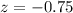
P-value of the test:
The pvalue of the test is the pvalue of z = -0.75, which is 0.2266
0.2266 > 0.01, which means that there is not sufficient evidence to support the claim that the bags are underfilled.