We are given with a quadratic equation and we have to factorise it , so let's proceed.
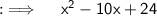
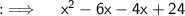
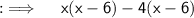
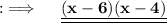
Used Concepts :-
To factorise a quadratic polynomial ax² + bx + c we have to split it's middle term bx into say mx and nx and it will look like ax² + mx + nx + c ,also we should split it such that it follows the both conditions below :-