Question

Tell whether the table of values represents a linear function, an exponential function, or a quadratic funtion

Answer 1

Explanation:

if it is linear then it will be a straight line(gradient is the same)

if quadratic then curve(gradeint isnt the same)

y=mx+c

m=[y(2)-y(1)]/[x(2)-x(1)]

you can choose any 2 points from the table

m=2-0.4/0-1

m=-1.6

repeat but 2 different coordinates

m=0.4-0.08/-1--2==>-2.24

m=-2.24

different coordinate therefore quadratic

cant be exponential, because nothing is being raised to some power

Answer 2

The table exhibits a constant ratio of 5 between consecutive y-values, suggesting an exponential relationship. Thus, the given values represent an exponential function.

To determine whether the table of values represents a linear function, an exponential function, or a quadratic function, let's examine the ratios between consecutive y-values and see if they follow a specific pattern.

Given the table:

`\text{x} & \quad \ \ \ \ \ \text{y} \\-2 & \quad 0.08 \\-1 & \quad 0.4 \\0 & \quad \ \ \ \ 2 \\1 & \quad \ \ \ 10 \\`

Let's calculate the ratios:

`\[\begin{align*}(0.4)/(0.08) & = 5 \\(2)/(0.4) & = 5 \\(10)/(2) & = 5 \\\end{align*}\]`
`(0.4)/(0.08) = 5 \\\\(2)/(0.4) = 5 \\\\(10)/(2) = 5 \\`

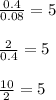
In this case, the ratios between consecutive y-values are the same (5 in each case). When the ratio between consecutive terms is constant, it indicates an exponential function. Therefore, the table of values represents an exponential function.