Answer:

Explanation:
x = Length and width of base
y = Height of box
Volume of the box is
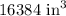
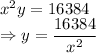
Surface area is given by

Differentiating with respect to x we get
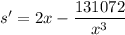
Equating with 0 we get
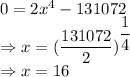
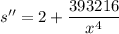
at
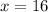

So the function is minimum at x = 16
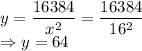
The material required is
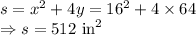
The minimum amount of material required is
 .
.