Answer:
the P-value = 0.1977
conclusion: Since the p-value is not small;
we reject null hypothesis
hence, the data does not support claim that more than half of the bathroom scales underestimate weight.
Explanation:
Given the data in the question;
let X represent the number of successes ( the weight is underestimated ) in n independent Bernoulli trials, each with the success probability p
X - Bin( n,p).
so
Null hypothesis H₀ : p ≤ 0.5
Alternative hypothesis Hₐ : p > 0.5
now, compute np₀ and n( 1 - p₀ )
np₀ = (50)(0.5)
np₀ = 25
n( 1-p₀ ) = (50)(1 - 0.5)
n( 1-p₀ ) = 25
we can see that both values are greater than 10.
∴ the sample proportion is approximately normally distributed;
P" - N ( p₀,
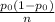 )
)
sample proportion p" = 28/50 = 0.56
standard deviation will be;
σ
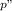 = √( p₀(1-p₀) / n )
= √( p₀(1-p₀) / n )
σ
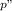 = √( 0.5(1-0.5) / 50 )
= √( 0.5(1-0.5) / 50 )
σ
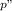 = √( 0.25 / 50 )
= √( 0.25 / 50 )
σ
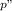 = 0.07071
= 0.07071
Next is the Z-score
z = p" - p₀ / σ
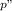
z = 0.56-0.5 / 0.07071
z = 0.06 / 0.07071
z = 0.85
from table,
the probability that a standard normal random variable takes on a value greater than 0.85 is approximately 0.1977
Therefore, the P-value = 0.1977
conclusion: Since the p-value is not small;
we reject null hypothesis
hence, the data does not support claim that more than half of the bathroom scales underestimate weight.
p = 0.197663