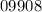Question

In a certain section of Southern California, the distribution of monthly rent for a one-bedroom apartment has a mean of $2,025 and a standard deviation of $230. The distribution of the monthly rent does not follow the normal distribution. In fact, it is positively skewed. What is the probability of selecting a sample of 60 one-bedroom apartments and finding the mean to be at least $1,955 per month

Answer 1

The probability is "0.9908". The further explanation is provided below.

Explanation:

The given values are:

Mean,

`\mu=2025`

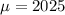
Standard deviation,

`\sigma =230`

Sample,

`n=60`

According to the question,

The probability of selecting a sample of 60 one-bedroom apartments will be:

=
`P(\frac{\bar{x}- \mu}{(\sigma)/(√(n) ) } \geq \frac{1955-2025}{\sqrt{(230)/(√(60) ) } } )`

=
`P(Z\geq -2.36)`

=
`1-P(Z \leq -2.36)`

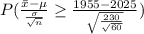
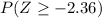
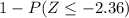
After placing the values, we get

=
`0.0092`

or

=
`09908`