Question

A 90-m3 basement in a residence is found to be contaminated with radon coming from the ground through the floor drains. The concentration of radon in the room is 1.5 Bq/L under steady-state conditions. The room behaves as a CSTR and the decay of radon is a first-order reaction with a decay rate constant of 2.09 3 1026 s21 . If the source of radon is closed off and the room is vented with radon-free air at a rate of 0.14 m3 /s, how long will it take to lower the radon concentration to an acceptable level of 0.15 Bq/L

Answer 1

25 minutes

Step-by-step explanation:

V = Volume =
`90\ \text{m}^3`

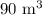
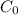`C_0` = Radon concentration under steady state = 1.5 Bq/L

k = Radon decay rate =
`2.09* 10^(-6)\ \text{s}^(-1)`

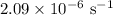
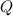`Q` = Venting rate =
`0.14\ \text{m}^3/\text{s}`

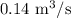
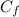`C_f` = Final concentration of radon = 0.15 Bq/L

Theoretical detention time is given by

`\theta=(V)/(Q)\\\Rightarrow \theta=(90)/(0.14)\\\Rightarrow \theta=642.86\ \text{s}`

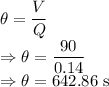
We have the relation

`C_f=C_0e^{-((1)/(\theta)+k)t}\\\Rightarrow t=(\ln(C_f)/(C_0))/(-((1)/(\theta)+k))\\\Rightarrow t=(\ln(0.15)/(1.5))/(-((1)/(642.86)+2.09* 10^(-6)))\\\Rightarrow t=1478.25\ \text{s}=(1478.25)/(60)=24.63\approx 25\text{minutes}`

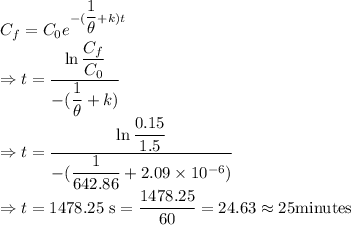
The time taken to reach the acceptable level of concentration is 25 minutes.