Question

the arc measure of a sector in a given circle is doubled. will the area of the sector also be doubled? explain your reason

Answer 1

Yes. See explanation below.

Explanation:

The central angle and the degree arc measure of a sector of a circle are equal. Doubling the arc measure, doubles the central angle measure and vice versa.

Area of the the original sector:

`A_(sector) = (n)/(360^\circ)\pi r^2`

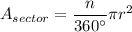
where n = measure of the central angle of the sector

Since the central angle and the arc measure of the sector are equal, changing the arc measure has the same effect as changing the central angle measure.

Let's double the central angle to 2n which is the same as doubling the arc measure.

Area of the sector with a doubled central angle or a doubled arc measure:

`A_(sector) = (2n)/(360^\circ)\pi r^2`

Now we divide the area of the doubled sector by the area of the original sector.

`((2n)/(360^\circ)\pi r^2)/((n)/(360^\circ)\pi r^2) =`

Simplify:

`= (2n)/(n) * (360^\circ \pi r^2)/(360^\circ \pi r^2)`

`= (2n)/(n)`

`= 2`

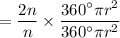
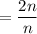
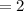
The ratio of the areas is 2, so the area of the sector is indeed doubled.

Answer: Yes.