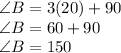Answer:
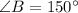
Explanation:
The diagram is two parallel lines cut by a transversal therefore Angle A and Angle B are alternate interior angles, in this case meaning they are equivalent (because lines are parallel).
We can use this information to set up an equation:
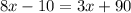
Add 10 to both sides:
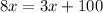
Subtract 3x from both sides
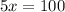
Divide both sides by 5
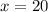
Then, substitute 20 for x to solve for Angle B: