Answer:
The equation of the midline for the function
 is
is
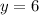 .
.
Explanation:
The sinusoidal function of the form
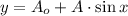 is a periodic function whose range is bounded between
is a periodic function whose range is bounded between
 (minimum) and
(minimum) and
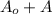 (maximum). The equation of the midline is a line paralel to the x-axis, that is:
(maximum). The equation of the midline is a line paralel to the x-axis, that is:
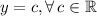 (1)
(1)
Where
 is mean of the upper and lower bounds of the sinusoidal function, that is:
is mean of the upper and lower bounds of the sinusoidal function, that is:
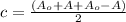
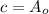 (2)
(2)
If we know that
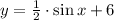 , then the equation of the midline for the function
, then the equation of the midline for the function
 is:
is:
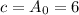
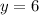
The equation of the midline for the function
 is
is
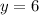 .
.