Answer:
The horizontal distance is 46.1 miles.
Explanation:
Here, the given question can be explained by the sides of a right angled triangle. Let x represent the horizontal miles, then applying an appropriate trigonometric function;
Tan θ =
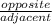
Tan
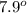 =
=
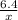
0.1388 =
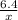
x =
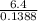
= 46.1095
x = 46.1 miles
The plane needs to travel a horizontal distance of 46.1 miles.