Question

Write a quadratic equation given the x intercepts and other other point. Put steps together. Find the factors. Solve for a by substituting in the extra point. Write the equation in factored form.

Answer 1

This question is clearly incomplete, so i will answer it in a really general way.

Suppose that for a quadratic function, we know that the x-intercepts are a and b.

And we also know that this function passes through the point (c, d).

First a definition, for a n-degree polynomial with the x-intercepts {x₁, x₂, ...,xₙ} and a leading coefficient K, we can write this polynomial in the factorized form as:

p(x) = K*(x - x₁)*(x - x₂)*...*(x - xₙ)

Now let's do the same for our quadratic function, we can write it as:

f(x) = K*(x - a)*(x - b)

(where a and b are known numbers)

Now we also know that this function passes through the point (c, d)

This means that:

f(c) = d

then:

d = K*(c - a)*(c - b)

With this equation we can find the value of K,

K = d/( (c-a)*(c - b))

Then the quadratic function is:

`f(x) = d((x-a))/((c-a)) ((x-b))/((c-b))`

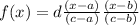
Where again, it is supposed that you know the values of a and b, and also the point (c, d)