Answer:
The amount of drug left in his body at 7:00 pm is 315.7 mg.
Step-by-step explanation:
First, we need to find the amount of drug in the body at 90 min by using the exponential decay equation:
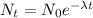
Where:
λ: is the decay constant =
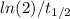
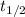 : is the half-life of the drug = 3.5 h
: is the half-life of the drug = 3.5 h
N(t): is the quantity of the drug at time t
N₀: is the initial quantity
After 90 min and before he takes the other 200 mg pill, we have:
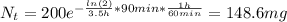
Now, at 7:00 pm we have:
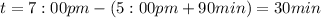
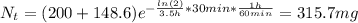
Therefore, the amount of drug left in his body at 7:00 pm is 315.7 mg (from an initial amount of 400 mg).
I hope it helps you!