Question

Each of the sides of a pentagon is 12 cm long. Two ants are walking from point A to point D along the sides of the pentagon. One ant walks from point A to point B to point C to point D at an average speed of 3 centimeters per second. The other ant walks from point A to point E to point D, arriving at point D at the same time as the first ant. What is the average speed of the second ant, in cm per second?

Answer 1

The average speed of the second ant is 2 cm/s

Explanation:

The details of the ants moving on the sides of the pentagon are;

The length of the sides of the pentagon = 12 cm

The path of the first ant = A to B, B to C, then C to D

The average speed of the first ant = 3 cm/s

The path of the second ant = A to E, and E to D

The time of arrival of the second ant at the point D = The time of arrival of the first ant at the point D

Given that both ants departed at the same time, from point A, we have;

The time it takes the first ant to arrive at the point D = The time it took the second ant to arrive at the point D

The distance from A to B = 12 cm

The distance from B to C = 12 cm

The distance from C to D = 12 cm

∴ The distance traveled by the first ant from A to D = 12 cm + 12 cm 12 cm = 36 cm

Average speed = (Total distance)/(Total Time)

Total time = (Total distance)/(Average speed)

Let 't' represent the time it takes the first ant to move from point A to point D, we have;

t = 36 cm/(3 cm/s) = 12 seconds

Therefore, the time it takes the first ant to move from point A to point D, t = 12 seconds = The time it takes the second ant to move from point A to point D through point E

The total distance traveled by the second ant from A to point E, then from point E to point D,
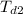`T_(d2)` = 12 cm + 12 cm = 24 cm

The average speed of the second ant, v₂ =
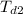`T_(d2)`/t

∴ v₂ = 24 cm/(12 seconds) = 2 cm/s

The average speed of the second ant, v₂ = 2 cm/s.