Answer:
The lenght of the chord is 8 cm.
Explanation:
The chord AB is 3 cm from the center of the circle. If we visualize the chord (in a horizontal position) and the radius of the circle (in a diagonal position) we can notice that both of them forms a triangle, with the following dimentions:
b: is the base =?
s: is one side of the triangle = distance of the chord from the center of the circle = 3 cm
h: is the hipotenuse = radius of the circle = 5 cm
To find the base (or the ohter side of the triangle) we need to use Pitagoras:
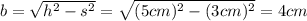
The above value is the half of the chord AB, so:

Therefore, the lenght of the chord is 8 cm.
I hope it helps you!