Answer:
A linear function in the form y = m·x + b for the line passing through the point (2, -4) with y-intercept 2 is;
y = -3·x + 2
Explanation:
From the question, it is required to find the a linear equation passing through the point (2, - 4) with a y-intercept 2 in the form y = m·x + c
Given that the y-intercept is the point at which the line cuts the y-axis, we have, x = 0
Therefore, we have the point on the line representing the y-intercept is (0, 2)
Therefore, the slope of the graph is given as follows;
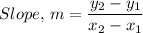
Therefore, we have;
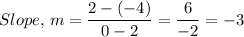
The equation of the graph in point and slope is given as follows;
y - 2 = -3 × (x - 0) = -3 × x
Therefore, the equation of the line in the form y = m·x + c is given as follows;
y - 2 + 2 = -3 × x + 2
∴ y = -3·x + 2
The equation of the line in the form y = m·x + c is y = -3·x + 2.