Question

HELPPPPPPPP this is due tonight!!!!!!!!

Answer 1

Answer: (n-1) + n + (n+1) = 3n

Step-by-step explanation: So, for this equation, plug in the integers 7, 8 and 9, preferably in order. The variable next to the 3 will be the second integer. (7-1) + 8 + (9+1) = 3(8). If you solve the equation, you will get 24=24, which is true. This is because since the integers are consecutive, you start out with like 24=24. Then you subtract from the left side, which becomes 23, and then you add 1 again to it, which becomes 24. Hopefully, you understand what I mean. It's a difficult concept to explain.

Answer 2

Explanation:

Let x be the first integer

Let y be the 2nd integer

Let z be the 3rd integer

Given

`x + y + z = 3y`

Also given, x = 7, y = 8, z = 9, substitute x,y and z into equation.

`x + y + z = 7 + 8 + 9 \\ = 24`

`3y = 3 * 8 \\ = 24`

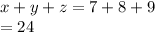
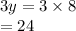
Therefore,

x+y+z = 3y for x = 7, y = 8, z = 9.

Now lets take x = 3, y = 4, z = 5.

`x + y + z = 3 + 4 + 5 \\ = 12`

`3y = 3 * 4 \\ = 12`

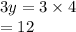
As you can see , x+y+z = 3y is true for any 3 consecutive numbers.