Question

Using the binomial theorem to expand (1+4x)^4​

Answer 1

`{256x}^(4)+{256x}^(3) + {96x}^(2) + 16x + 1`

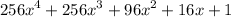
Step-by-step explanation:

`{(1 + 4x)}^(4) = (1 + 4x)(1 + 4x)(1 + 4x)(1 + 4x)`

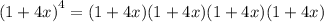
The coefficient of the kth term (ordering in increasing order for the exponent of x) is just the number of ways we have to choose k factors from that expression, so if we let k be the exponent of x, and n be the total number of terms, the coefficient of x^k is
`\binom{n}{k} = (n!)/(k!(n-k)!)`

Which, of course, we have to multiply for the product of the two terms.

For example, the coefficient of the third grade term in
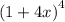`{(1+4x)}^(4)` is
`\binom{4}{3}=4`

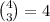
So we have
`{(1 + 4x)}^(4) = \binom{4}{4} \cdot {(4x)}^(4)+\binom{4}{3} \cdot {(4x)}^(3) + \binom{4}{2} \cdot {(4x)}^(2) + \binom{4}{1} \cdot 4x + \binom{4}{0} \cdot 1`

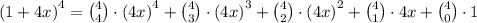
Which is equal to
`1 \cdot {(4x)}^(4)+4 \cdot {(4x)}^(3) + 6 \cdot {(4x)}^(2) + 4 \cdot 4x + 1 \cdot 1 = {256x}^(4)+{256x}^(3) + {96x}^(2) + 16x + 1`

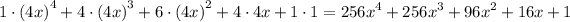
Hope this helps :)