Explanation:
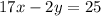
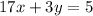
Both equations have a
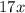 term in them, so if we subtract the second equation from the first, it will eliminate those terms, allowing us to solve for the remaining
term in them, so if we subtract the second equation from the first, it will eliminate those terms, allowing us to solve for the remaining
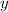 terms:
terms:
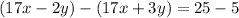
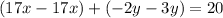
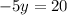
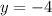
Finally, we can plug this value for
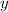 into either of the two original equations to solve for
into either of the two original equations to solve for
 :
:
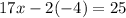
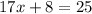
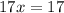
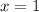
This means the solution to the system of equations is
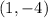 .
.