Question

Two point charges are placed on the x axis. 4 µC at x = 0.2 m and -5 µC at x = -0.2 m. Determine the magnitude and direction of the electric field on y axis at y = 0.15 m.

Answer 1

E = 10.10 10⁵ N / C, θ = 184.75º

Step-by-step explanation:

The electric field created by a point charge is

E = k q / r²

where r is the distance from the load to the desired point

Since the electric field is a vector quantity, one of the simplest ways to calculate it is to find the components of the electric field on each axis and add them.

charge 1 q₁ = 4 10⁻⁶ C placed at position x₁ = 0.2 m

the distance is

r² = (x-x₀) ² + (y-y₀) ²

r² = (0 - 0.2) ² + (0.15 - 0) ²

r² = 0.0625

E₁ = 9 10⁹ 4 10⁻⁶ / 0.0625

E₁ = 5.76 10⁵ N / C

let's find the angle of this vector

tan θ = y / x

θ = tan⁻¹ y / x

θ = tan⁻¹ 0.15 / 0.2

θ = 36.9º

This angle is in the second quadrant since as the load is positive the electric field is salient, this angle measured from the positive side of the x axis is

θ’= 180- θ

θ’= 180- 36.9

θ’= 143.1º

we use trigonometry

cos 143.1 = E₁ₓ / E₁

sin 143.1 = E_{1y} / E₁

E₁ₓ = E₁ cos 143.1

E_{1y} = E₁ sin 143.1

E₁ₓ = 5.76 10⁵ cos 143.1 = -4.606 10⁵ N / C

E_{1y} = 5.76 10⁵ sin 143.1 = 3.458 10⁵ N / C

charge 2 q₂ = 5 10⁻⁶ at position x = -0.2 m

r²2 = 0.2² + 0.15²

r² = 0.0625

E₂ = 9.10⁹ 5 10⁻⁶/0.0625

E₂ = 7.20 10⁵ N / c

we look for the angles

tan θ = y / x

θ = tan⁻¹ 0.15 / 0.2

θ = 36.9º

in that case the charge is negative, therefore the electric field is directed to the charge and therefore the angle is in the third quadrant

θ'= 180 + θ

tea = 180 + 36.9 = 216.9º

the components of the electric field are

E₂ₓ = E₂ cos 216.9

E_{2y} = E₂ sin 216.9

E₂ₓ = 7.20 10⁵ cos 216.9 = -5.76 10⁵ N / C

E_{2y} = 7.20 10⁵ sin 216.9 = -4.32 10⁵ N / C

The components of the total electric field are

Eₓ = E₁ₓ + E₂ₓ

Eₓ = -4.606 10⁵ -5.76 10⁵

Eₓ = - 10,366 10⁵ N / C

E_y = E_{1y} + E_{2y}

E_y = 3.458 10⁵ -4.32 10⁵

E_y = -0.862 10⁵ N / C

We can give the result in two ways

1) E = Ex i ^ + Ey j ^

E = (- 10.366 i ^ -0.862 j ^) 10⁵ N / C

2) in the form of module and angle

let's use the Pythagorean theorem

E =
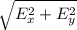`√(E_x^2 + E_y^2 )`Ra Ex² + Ey²

E =
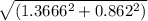`√( (1.3666^2 + 0.862^2))` 10⁵

E = 10.10 10⁵ N / C

trigonometry

tan θ’= E_y / Eₓ

θ'= tan⁻¹ (0.862 / 10366)

θ’= 4.75º

this angle is in the third quadrant, therefore measured from the positive side of the x-axis is

θ = 180 + θ'

θ = 180 + 4.75

θ = 184.75º