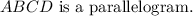Answer:
See Below.
Explanation:
We are given that A, B, C, and D are the midpoints of sides PQ, QR, RS, and SP, respectively.
And we want to prove that ABCD is a parallelogram.
By the definition of midpoint, this means that:
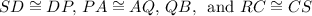
To prove, we can construct a segment from S to Q to form SQ. This is shown in the first diagram.
By the Midpoint Theorem:

Similarly:
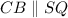
By the transitive property for parallel lines:
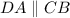
Likewise, we can do the same for the other pair of sides. We will construct a segment from P to R to form PR. This is shown in the second diagram.
By the Midpoint Theorem:
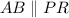
Similarly:

So:
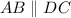
This yields:
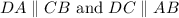
By the definition of a parallelogram, it follows that: