Question

Three charged particles of charges 3 μC, -2 μC, and 4 μC are placed on the X-Y plane at (1 cm, 0), (2.5 cm, 0), and (1 cm, 2 cm) respectively. Determine the magnitude and direction of the force acting on a -2 μC charge.

Answer 1

The total force is
`F_(tot)=4.29\: N`

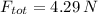
The direction is
`\omega=32.43^(\circ)`

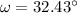
Step-by-step explanation:

First, we need to find the angle with respect to the horizontal, of the force between q2 (-2 μC) and q3 (3 μC).

Let's use the tangent function.

`tan(\alpha)=(2)/(1.5)`

`\alpha=53.13^(\circ)`

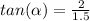
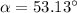
Now, let's find the magnitude of the force F(12).

`|F_(12)|=k(q_(1)q_(2))/(d_(12))`

Where:

• k is the Coulomb constant (9*10⁹ NC²/m²)
• q1 is 3 μC
• q2 -2 μC
• d(12) is the distance between q1 and q2 ( 1.5 cm = 0.015 m)

`|F_(12)|=9*10^(9)(3*10^(-6)*2*10^(-6))/(0.015)`

`|F_(12)|=3.6\: N`

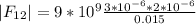
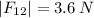
The magnitude of the force F(23) will be:

`|F_(23)|=k(q_(2)q_(3))/(d_(23))`

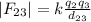
The distance between these charges is:

`d_(23)=\sqrt{1.5^(2)+2^(2)}`

`d_(23)=2.5\: m`

`|F_(23)|=9*10^(9)(2*10^(-6)*4*10^(-6))/(0.025)`

`|F_(23)|=2.88\: N`

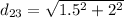
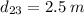
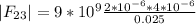
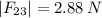
So, we have the force F(12) in the second quadrant and F(23) in the second quadrant too but with 53.13 ° with respect to the horizontal.

We just need to add these two forces (vectors) and get the total force acting on q2.

Total force in x-direction:

`F_(tot-x)=-F_(12)-F_(23)cos(53.13)`

`F_(tot-x)=-3.6-2.88cos(53.13)`

`F_(tot-x)=-5.33\: N`

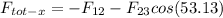
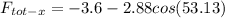
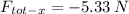
Total force in y-direction:

`F_(tot-y)=F_(23)sin(53.13)`

`F_(tot-y)=2.88sin(53.13)`

`F_(tot-y)=2.3\: N`

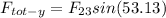
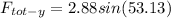
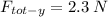
Therefore, the magnitude of the total force will be:

`|F_(tot)|=\sqrt{(-3.62)^(2)+(2.3)^(2)}`

`|F_(tot)|=4.29\: N`

and the direction is:

`tan(\omega)=(2.30)/(3.62)`

`\omega=32.43^(\circ)`

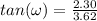
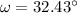
I hope it helps you!