Answer:
The answer is below
Explanation:
The z score is used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by the formula:

Therefore given that μ = $85900, σ = $11000, n = 35.
For x > 70000:
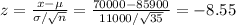
For x < 100000
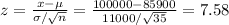
From the normal distribution table, P(70000< x < 100000) = P(-8.55 < z < 7.58) = P(z < 7.58) - P(z < -8.55) = 1 - 0 = 1 = 100%