Answer:
see explanation
Explanation:
(1)
The common ratio r of a geometric sequence is
r =
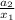 =
=
 , so
, so
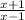 =
=
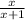 ( cross- multiply )
( cross- multiply )
(x + 1)² = x(x - 1) ← expand both sides
x² + 2x + 1 = x² - x ( subtract x² - x from both sides )
3x + 1 = 0 ( subtract 1 from both sides )
3x = - 1 ( divide both sides by 3 )
x = -

(2)
r =
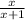 =
=
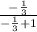 =
=
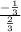 = -
= -

(3)
If - 1 < r < 1 then the sequence will converge
r = -
 meets this criteria , thus the sequence is convergent
meets this criteria , thus the sequence is convergent