Question

Write the explicit formula for the arithmetic sequence below and use it to find the 52nd term: 25, 19, 13, 7

Answer 1

`\displaystyle \:a_n=- 6n + 31`

`\displaystyle \:a_(52)= - 281`

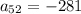
Explanation:

we are given some numbers

25,19,13,9

and said to figure out the sequence and 52 term

recall arithmetic sequence

`\displaystyle \: a + (n - 1)d`

where a is the first term and d is the common difference

let's figure out d

`\displaystyle \:d = 19 - 25 \\ d= - 6`

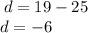
and a is 25

now we need to substitute the value of a and d and simplify to get our formula

substitute the value of a and d:

`\displaystyle \: 25 + (n - 1) (- 6)`

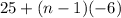
distribute -6:

`\displaystyle \: 25 + ( - 6n + 6)`

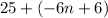
remove parentheses:

`\displaystyle \: 25 - 6n + 6`

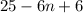
simplify addition:

`\displaystyle \: - 6n + 31`

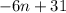
so our formula is -6n+31

remember here n means nth number term

we are said to figure out 52 number term

so

substitute the value of n:

`\displaystyle \: - 6.52 + 31`

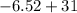
simplify multiplication:

`\displaystyle \: - 312 + 31`

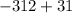
simplify addition:

`\displaystyle \: - 281`