Answer:
The value of the machine after two years is approximately $466.6
Explanation:
The details of the valuation of the machine are;
The function giving the machine value, 'V', is V =
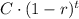
Where;
C = The original cost of the machine
r = The depreciation rate
t = The time the machine has been in service
When C = $576, r = 0.1, t = 2 years, we have;
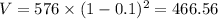
Therefore, the value of the machine that costs $576 having a depreciation of 0.1 after 2 years is, V = $466.58
By rounding to the nearest cent, we have, V = $466.6.