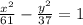Question

A hyperbola centered at the origin has verticies at (add or subtract square root of 61,0 and foci at (add or subtract square root of 98,0

Answer 1

`(x^2)/(61)-(y^2)/(37) =1`

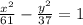
Explanation:

The standard equation of a hyperbola is given by:

`((x-h)^2)/(a^2) -((y-k)^2)/(b^2) =1`

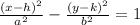
where (h, k) is the center, the vertex is at (h ± a, k), the foci is at (h ± c, k) and c² = a² + b²

Since the hyperbola is centered at the origin, hence (h, k) = (0, 0)

The vertices is (h ± a, k) = (±√61, 0). Therefore a = √61

The foci is (h ± c, k) = (±√98, 0). Therefore c = √98

Hence:

c² = a² + b²

(√98)² = (√61)² + b²

98 = 61 + b²

b² = 37

b = √37

Hence the equation of the hyperbola is:

`(x^2)/(61)-(y^2)/(37) =1`