Question

A swing base is 72 cm above the ground as shown in figure. When it travels through an angle of 60∘ from its mean position, swing base comes at 252 cm above the ground. What is the length of the arc travelled by the swing in meters?​

Answer 1

The length of the arc travelled by the swing is approximately 3.77 m

Explanation:

The given parameters of the swing are;

The swing base height of the swing above the ground = 72 cm

The swing base height above the when the swing travels an angle of 60° = 252 cm

Therefore we have;

r × cos(60°) = r - 180

180 = r - r × cos(60°)

r = 180/(1 - cos(60°)) = 360

r = 360 cm

The length of the arc travelled by the swing in meters,
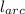`l_(arc)` is given as follows;

`l_(arc) = (\theta)/(360 ^(\circ)) * \pi * 2* r`

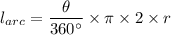
Therefore;

`l_(arc) = (60^(\circ))/(360 ^(\circ)) * \pi * 2*360 = (1)/(6) * \pi * 720 = 120 \cdot \pi`

The length of the arc travelled by the swing,
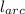`l_(arc)` = 120·π cm

∴ The length of the arc travelled by the swing,
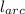`l_(arc)` = 1.2·π m ≈ 3.77 m