Answer:
a. r = 8 cm
b. The volume of the cone is approximately 1,229 cm³
Explanation:
The given parameters are;
The slant height of the cone = l cm
The base radius of the cone = r cm
The total surface area of the cone = 224·π cm
r : l = 2 : 5
Therefore, we have;
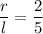

The total surface area of a cone, T.S.A. = π·r·l + π·r²
The total surface area of the cone, T.S.A. cone = π × (2/5)·l² + π·((2/5)·l)²
T.S.A. cone = π × (2/5)·l² + π·((2/5)·l)² = π·((2/5)·l² + (4/25)·l²)
T.S.A. cone = π·l²·((2/5) + (4/25)) = (14/25)·π·l²
∴ T.S.A. cone = 224·π cm² = (14/25)·π·l²
l² = 224 cm² × 25/14 = 400 cm²
l = √(400 cm²) = 20 cm
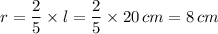
r = 8 cm
b. The volume of a cone, V = 1/3·π·r²·h
Where;
h = The height of the cone
By Pythagoras's theorem, h = √(l² - r²)
∴ h = √(20² - 8²) = √(336) = 4·√(21)
The height of the cone, h = 4·√(21)
The volume of the cone, V = 1/3 × (22/7) × 8² × 4·√(21) ≈ 1,229.00315781
∴ The volume of the cone, V to the nearest whole number ≈ 1,229 cm³.