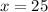Question

Can SOMEBODYYY please do the maths!!! PLeassssssssssssseeeeeeee

Answer 1

see below

Explanation:

Question-6:

we are given a equation

`\sf \displaystyle \: \log_(4)( - x) + \log_(4)( 6 - x) = 2`

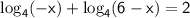
to solve so

recall logarithm multiplication law:

`\sf \displaystyle \: \log_(4)( - x * (6 - x)) = 2`

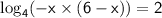
simplify multiplication:

`\sf \displaystyle \: \log_(4)( - 6 x + {x}^(2) ) = 2`

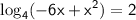
remember
`\displaystyle \log_(4)(4^2)=2`

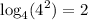
so

`\sf \displaystyle \: \log_(4)( - 6 x + {x}^(2) ) = \log_(4)( {4}^(2) )`

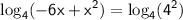
cancel out
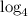`\log_4` from both sides:

`\sf \displaystyle \: - 6 x + {x}^(2) = {4}^(2)`

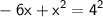
simplify squares:

`\sf \displaystyle \: - 6 x + {x}^(2) = 16`

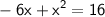
move left hand side expression to right hand side and change its sign:

since we are moving left hand side expression to right hand side there'll be only 0 left in the left hand side

`\sf \displaystyle \: - 6 x + {x}^(2) - 16 = 0`

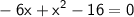
rewrite it to standard form i.e ax²+bx+c=0

`\sf \displaystyle \: {x}^(2) - 6x - 16 = 0`

rewrite -6x as 2x-8x:

`\sf \displaystyle \: {x}^(2) + 2x - 8x - 16 = 0`

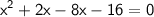
factor out x and 8:

`\sf \displaystyle \: x {(x}^{} + 2) - 8(x + 2) = 0`

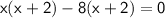
group:

`\sf \displaystyle \: (x - 8){(x}^{} + 2) = 0`

`\displaystyle \: x = 8 \\ x = - 2`

`\therefore \: x = - 2`

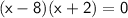
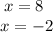
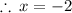
Question-7:

move left hand side log to right hand side:

`\displaystyle \: \log(x ) + \log(x - 21) = 2`

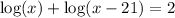
use mutilation logarithm rule;

`\displaystyle \: \log( {x}^(2) - 21x) = 2`

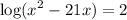
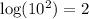`\log(10^2)=2` so

`\displaystyle \: \log( {x}^(2) - 21x) = \log({10}^(2) )`

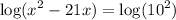
cancel out log from both sides:

`\displaystyle \: {x}^(2) - 21x = 100`

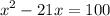
make it standard form:

`\displaystyle \: {x}^(2) - 21x - 100= 0`

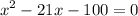
factor:

`\displaystyle \: {(x} + 4)(x - 25)= 0`

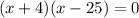
so

`\displaystyle \: x = 25`