Answer:
5,000 square feet
Skills Needed: 2-D Geometry
Explanation:
1) First, it says that 300 ft is the total amount of wire used to build the rectangular plot. This means that 300 is the perimeter of the plot. It is the length of the entire boundary of the shape.
---> The formula for perimeter is:
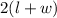 for a rectangle.
for a rectangle.
2) We can use the perimeter formula to the find the length and width, and then use the area formula to find the area. Area is the total amount of space taken up by the figure in 2 dimensions.
---> Area formula is:
 for a rectangle
for a rectangle
3) We are given that the length is 2 times as much as (or twice as much as) the width.
--->
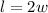
Using perimeter formula:
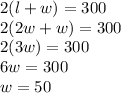
We substitute in for length and then solve for width as shown above.
Given the width, we can solve for length using the fact that length is twice the width.
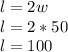
We use substitution to solve for length.
4) Now given length is 100, and with is 50, we can use the area formula.
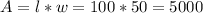
This means the area is 5000 square feet.