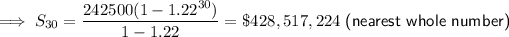Answer:
total profit = $428,517,224 (nearest whole number)
Explanation:
Use geometric sum formula:
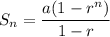
where
 is the initial value and
is the initial value and
 is the common ratio
is the common ratio
We have been told that the initial value is 242500, so
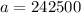 .
.
If the company's profit increases by 22% per year, this means each year's profit is 122% of the previous year's profit. 122% = 122/100 = 1.22
Therefore,
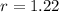
We need to calculate the total profit earned over 30 years, so

Inputting these values into the formula: