Given:
f(x) is an exponential function where f(3) = 18 and f(7.5) = 60.
To find:
The value of f(12), to the nearest hundredth.
Solution:
Let the exponential function be
 ...(i)
...(i)
It is given that
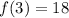 . Substitute
. Substitute
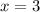 in (i).
in (i).

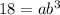 ...(ii)
...(ii)
It is given that
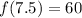 . Substitute
. Substitute
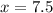 in (i).
in (i).
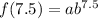
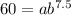 ...(iii)
...(iii)
Divide (iii) by (ii).
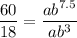
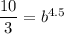
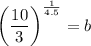

Putting
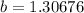 in (ii), we get
in (ii), we get
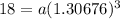
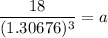

Putting
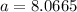 and
and
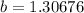 in (i), we get
in (i), we get
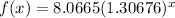
Putting x=12, we get
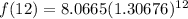

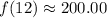
Therefore, the value of f(12) is about 200.00.