Answer:
1) (6, 0), (0, 3)
2) -½
3) y= -½x +3
4) -½
5) 2
Explanation:
1) x- intercept is the point at which the line passes though the x-axis.
From the graph, the x- intercept is (6, 0).
The y-intercept is the point at which the line passes through the y- axis.
From the graph, the y-intercept is (0, 3).
2) To find the slope, plug in the coordinates of any two points on the line into the gradient formula below.
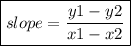
I will use the 2 points that they have provided to calculate the slope.
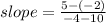
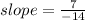
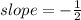
3) The equation of a line can be written as y= mx +c, where m is the gradient and c is the y-intercept.
Since we have already found those values in the previous questions, let's substitute them into the equation.

4) Parallel lines have the same slope.
Thus, the slope of a line parallel to the line in the graph will also have a slope of -½.
5) The product of the gradients of perpendicular lines is -1.
(gradient of perpendicular line)(-½)= -1
Gradient of perpendicular line
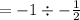
= 2