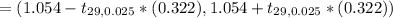Question

Measuring the height of a tree is usually more difficult than measuring the diameter of the tree. Therefore, many researchers use regression models to predict the height of a tree from its diameter measured at 4 feet 6 inches from the ground. The following computer output shows the results of a linear regression based on the heights, in feet, and the diameters in inches, recorded from 31 felled trees.

Estimate Std Error t-value Pr(>|t|)
Intercept 62.031 4.383 14.15 0.0000
Diameter 1.054 0.322 0.0028 3.27
Which of the following is a 95 percent confidence interval for the slope of the population regression line?
(A) (0.001.2.107).
(B) (0.396, 1.712.
(C) (0.423,1.685).
(D) (0.732. 1.376).
(E) (53.07.70.99).

Answer 1

(B) (0.396, 1.712)

Explanation:

From the information given;

Confidence Interval = 0.95

Significance Level
`= 1 - 0.95 = 0.05`

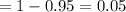
The confidence interval for regression coefficient beta (whereby in this case it is the coefficient of the diameter) is expressed by:

=
`( Beta ^- \ t_(n-2), \alpha/2 ( S.E \ of \ \^ \ \ ), Beta^+ \ t_(n-2), \alpha/2 ( S.E \ of \ \^ \ \ ))`

From the regression coefficient, the estimated value of beta^ = 1.054

`= (1.054 - t_(29,0.025) *(0.322), 1.054 + t_(29,0.025)*(0.322))`

`t_(229,0.025) = 2.0452\\\\ = \mathbf{(0.396, 1.712)}`