Solution :
According to the question, let
A : winning first scholarship
B : winning second scholarship
So for the first scholarship, there are five finalist and only two scholarship will be awarded. And for the second scholarship there are five finalist and only one scholarship will be awarded.
Therefore,
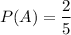 and
and
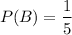
1. So,
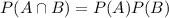
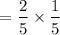
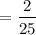
2.
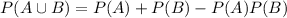
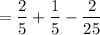
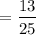
3. She should apply to both the scholarships, so as to have a maximum chances of winning at least one scholarship.