Answer:
![[H_3O^+]=4.7x10^(-3)M](https://img.qammunity.org/2022/formulas/chemistry/high-school/7ap158urie6tlcappf1i6x97czb7eewohn.png)
Step-by-step explanation:
Hello there!
In this case, since the ionization of benzoic acid is:
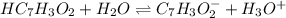
Whereas the corresponding equilibrium expression is:
![Ka=([C_7H_3O_2^-][H_3O^+])/([HC_7H_3O_2])](https://img.qammunity.org/2022/formulas/chemistry/high-school/kdm7lgj3g0o78hgeq8fuxlv9m7h5lx4yka.png)
Now, we insert the acidic equilibrium constant and the reaction extent x, to write:
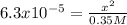
Thus, by solving for x, we obtain:
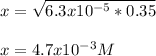
Which is also:
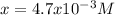
Best regards!