Answer:
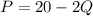
Step-by-step explanation:
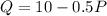
Price function can be estimated by inverting the demand function.
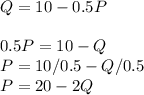
This is the price function.
Total revenue function can be estimated using the given formula,
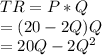
The linear demand function is given by,
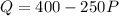
Price function is given by,
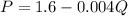
Total revenue function is thus given by,
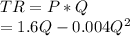
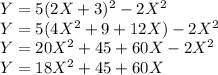
The derivative of Y with respect to x is,
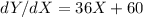
Equating this equal to 0 we get,
