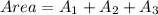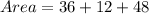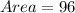Answer:
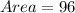
Explanation:
Given
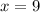
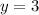

See attachment for rhombus
Required
Determine the area
From the attached rhombus:
We have
(1) Triangle
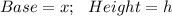
The area is:
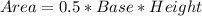
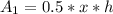
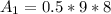
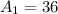
(2) Triangle
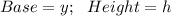
The area is:
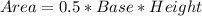
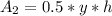
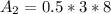

(3) Rectangle
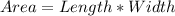
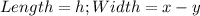
because all sides are equal, so the remaining side is x - y
So:

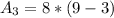
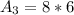

So, the area is: