Answer:
a)
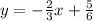
b)
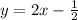
These two paths are not perpendicular to each other.
Explanation:
Equation of a line:
The equation of a line has the following format:

In which m is the slope of the line and b is the y-intercept.
If two lines are perpendicular, the multiplication of their slopes is -1.
(a) the engineering lab and the computer center
Coordinates (3.5,-1.5) and (0.5,0.5)
The slope is given by the change in y divided by the change in x.
Change in y: 0.5 - (-1.5) = 0.5 + 1.5 = 2
Change in x: 0.5 - 3.5 = -3
Slope:

So
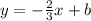
Now, to find the y-intercept, we replace one of these points into the equation.
(0.5,0.5) means that when
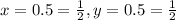
So
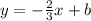

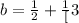
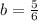
So
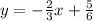
(b) the engineering lab with the library.
(0.5,0.5) and (-1,-2.5).
First, we find the slope:
Change in y:-2.5 - 0.5 = -3
Change in x: -1 - 0.5 = -1.5
The slope is:
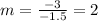
So
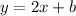
Now we find b
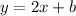
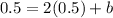
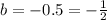
So
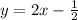
The multiplication of their slopes, is
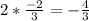
Since it is different of one, these paths are not perpendicular to each other.