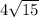Answer:
The shortest possible perimeter is:
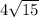
Explanation:
Given
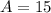 --- area
--- area
Required
Find the shortest possible perimeter
Area is calculated as:
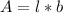
This gives:

Make l the subject
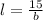
Perimeter is calculated as:
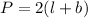
Substitute
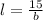

Rewrite as:
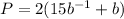
Differentiate and minimize;
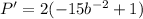
Minimize by equating P' to 0
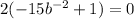
Divide through by 2
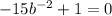

Divide through by -1
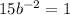
Rewrite as:
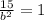
Solve for b^2
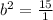
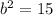
Solve for b
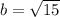
Recall that:

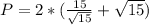
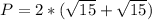
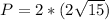
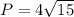
The shortest possible perimeter is: