Question

Consider a large truck carrying a heavy load, such as steel beams. A significant hazard for the driver is that the load may slide forward, crushing the cab, if the truck stops suddenly in an accident or even in braking. Assume, for example, that a 10000-kg load sits on the flatbed of a 20000-kg truck moving at 12.0 m/s. Assume that the load is not tied down to the truck, but has a coefficient of static friction of 0.500 with the flatbed of the truck.

(a) Calculate the minimum stopping distance for which the load will not slide forward relative to the truck.
(b) Is any piece of data unnecessary for the solution?

Answer 1

`14.68\ \text{m}`

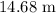
Masses of the truck and load

Step-by-step explanation:

v = Final velocity = 0

u = Initial velocity = 12 m/s

`\mu` = Coefficient of friction = 0.5

a = Acceleration

g = Acceleration due to gravity =
`9.81\ \text{m/s}^2`

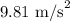
s = Displacement

f = Friction

F = Force applied

The force balance of the system is given by

`F=-f\\\Rightarrow ma=-\mu mg\\\Rightarrow a=-\mu g`

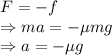
From the kinematic equations we have

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2(-\mu g))\\\Rightarrow s=(0-12^2)/(2(-0.5* 9.81))\\\Rightarrow s=14.68\ \text{m}`

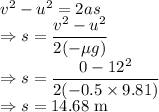
The minimum stopping distance for which the load will not slide forward relative to the truck is
`14.68\ \text{m}`

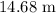
As it can be seen that the masses of the truck and load are not used in the above used formulae. So, they are unnecessary.