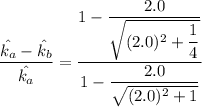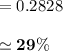Question

Suppose you design an apparatus in which a uniformly charged disk of radius R is to produce an electric field. The field magnitude is most important along the central perpendicular axis of the disk, at a point P at distance 2.00R from the disk. Cost analysis suggests that you switch to a ring of the same outer radius R but with inner radius R/2.00 . Assume that the ring will have the same surface charge density as the original disk. If you switch to the ring, by what percentage will you decrease the electric field magnitude at P?

Answer 1

The electric field will be decreased by 29%

Step-by-step explanation:

The distance between point P from the distance z = 2.0 R

Inner radius = R/2

Outer raidus = R

Thus;

The electrical field due to disk is:

`\hat {K_a} = (\sigma)/(2 \varepsilon _o) \Big( 1 - (z)/(√(z^2+R_i^2)) \Big)`)

`\implies (\sigma)/(2 \vaepsilon _o) \Big ( 1 - (2.0 \ R)/(√( (2.0\ R)^2+(R)^2)) \Big)`

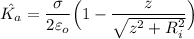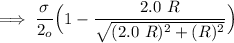
Similarly;

`\hat {K_b} = \hat {k_a} - (\sigma)/(2 \varepsilon_o) \Big( 1 - \frac{2.0 \ R}{\sqrt{(2.0 \ r)^2 + ((R)/(2)^2)}}\Big)`

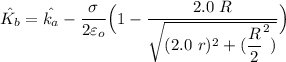
However; the relative difference is:
`\frac{\hat {k_a} - \hat {k_b}}{\hat {k_a} }= \frac{E_a -E_a + \frac{\sigma}{2 \varepsilon_o \Big[1 - \frac{2.0 \ R}{\sqrt{(2.0 \ R)^2 + ((R)/(2))^2}} \Big] } } { (\sigma)/(2 \varepsilon_o \Big [ 1 - (2.0 \ R)/(√( (2.0 \ R)^2 + (R)^2)) \Big] )}`

`\frac{\hat {k_a} - \hat {k_b}}{\hat {k_a} }= \frac{1 - \frac{2.0}{\sqrt{(2.0)^2 + (1)/(4)}} }{1 - (2.0 )/(√((2.0)^2 + 1))}`

`= 0.2828 \\ \\ \mathbf{\simeq 29\%}`